
The section plane minor axis offset length can be used to locate the center of the ellipse if your drawing out section planes, like W & A Mowat. The pitch of the plank can be used to check your geometric drawing of the tangent handrail system, if your drawing is based on Robert Riddell's embodying the perfect elucidation of the tangent system.
Tangent Handrailing Section Planes Tetrahedrons
50 pages of drawings on the study of Tangent Handrailing
Tangent Handrailing Fold out Poster Board Drawings
for 15 different plan tangents



Elucidation of the Tangent Handrailing Angles
Plan View Radius = 8.04494
Upper Tangent Angle = 50.56066°
Lower Tangent Angle = 39.12785°
Central Angle = 105°
Plan View Angle = 75°
cord = 2 * Radius * sin(central angle ÷ 2) = 12.76496
tangent length = (Radius* sin(central angle ÷ 2)) ÷ cos(central angle ÷ 2) = 10.48436
lower tangent rise = tangent length * tan(lower tangent angle)
lower tangent rise = 10.48436 * tan(39.12785) = 8.52888
tangent base offset = lower tangent rise ÷ tan(upper tangent angle)
tangent base offset= 8.52888 ÷ tan(50.56066) = 7.015515
upper tangent base =tangent length + tangent base offset upper tangent base = 10.48436 + 7.015515 = 17.49988
upper tangent height = upper tangent base * tan(upper tangent angle)
upper tangent height= 17.49988 * tan(50.56066) = 21.2749033461
ordinate length = square root ((cord² +upper tangent base² ) - (2 * cord * upper tangent base * cos(central angle ÷ 2))
ordinate length = square root ((469.1900038160 ) - (2 * 12.76496 * 17.49988 * cos(52.5))
ordinate length = square root ((469.1900038160 ) - (271.9766701837) = 14.0432664873
angle D = arccos((upper tangent base² + ordinate length² - cord²) ÷ (2 * upper tangent base * ordinate length) )
angle D = arccos((17.49988² + 14.0432664873² - 12.76496²) ÷ (2 * 17.49988 * 14.0432664873) )
angle D = arccos((340.515206998) ÷ (491.511223015)) = 46.148445275
angle DD = 180° - central angle - angle D
angle DD = 180°- 105- 46.148445275 = 28.851554725
seat = (Radius* cos(angle DD)) + (Radius* cos(angle D))
seat= (8.04494 * cos(28.851554725)) + (8.04494 * cos(46.148445275)) = 12.6195363496
pitch of plank = arctan(upper tangent height ÷ seat)
pitch of plank = arctan(21.2749033461 ÷ 12.6195363496) = 59.3250488281
semi-major axis = Radius ÷ cos(pitch of plank)
semi-major axis = 8.04494 ÷ cos(59.3250488281) = 15.7692298976
slant_angle = upper_tangent_angle
SS = arctan(tan(slant_angle) ÷ sin(Angle_DD))
S = atan(tan(slant_angle) ÷ sin(Angle_D))
Plan View Minor Axis Offset Length = radius * cos(Angle_D)
Section Plane Minor Axis Offset Length = Plan View Minor Axis Offset Length ÷ cos(SS)
major_axis = radius ÷ cos(SS)
utb = 90° - arctan(sin(upper_tangent_angle) ÷ tan(Angle_DD))
ltb = 90° - arctan(sin(lower_tangent_angle) ÷ tan(Angle_D))
R1 = arctan( tan(upper_tangent_angle) ÷ sin(Angle_DD))
R4Pm = arctan( cos(R1) ÷ tan(Angle_DD))
R4Pa = arctan( cos(R1) ÷ tan(Angle_D))
Angle of the Tangents = 180 - R4Pm - R4Pa
Understanding Tangent Handrailing
The file-- Tangent-Handrailing-Section-Planes-Tetrahedrons.pdf now contains:
Plates
1: Quarter Circle Plan with Equally Pitched Tangents.
2: Quarter Circle Plan with Short Lower Pitched Tangent.
3: Quarter Circle Plan with the Upper Tangent being Pitched with Level lower Tangent.
4: Quarter Circle Plan with the Upper Tangent Level with Pitched lower Tangent.
5: Quarter Circle Plan with Short Upper Pitched Tangent.
6: - 15: Yet To do.
16: Quarter Circle Plan with Short Lower Pitched Tangent, correct way to find twist bevel angles.
17: Obtuse Plan with Short Lower Pitched Tangent, correct way to find twist bevel angles.
18: Acute Plan with Short Lower Pitched Tangent, correct way to find twist bevel angles.
19.1: Tangent Handrailing Folding Template. This is the correct way to make a folding template for equal or unequally pitched tangents.
19: Tangent Handrailing Folding Template. Tetrahedron folding template for equal or unequally pitched tangents.
20: Tangent Handrailing trigonometry code to calculate the plan angles, major axis of the ellipse, upper and lower twist bevel angles and angle of the tangents.
21: Tangent Handrailing tetrahedron relationships to the dihedral angle and twist bevel angles.
22: Rotated Section Planes for Quarter Circle Plan with Equally Pitched Tangents.
23: Rotated Section Planes for Quarter Circle Plan with Unequal Pitched Tangents.
24: Rotated Section Planes for Obtuse Plan with Equally Pitched Tangents.
25: Rotated Section Planes for Obtuse Plan with Unequal Pitched Tangents.
26: Rotated Section Planes for Acute Plan with Equally Pitched Tangents.
27: Rotated Section Planes for Acute Plan with Unequal Pitched Tangents.
28: Step by step instructions for drawing Equally Pitched Tangents.
29: Tangent to Ellipse Geometric Drawing Instructions
30: The Tangent, Bevel and Elliptic Curve
From New Elements of Hand-Railing, by Robert Riddell 1871
31: The Ordinate, its Power and value in the Construction of Wreaths
From New Elements of Hand-Railing, by Robert Riddell 1871



 √ X + 1
√ X + 1
 | SBE Builders |

The book includes step by step instructions on developing stereotomic drawings on Art du Trait de Charpente, Trestles, Tréteau à devers, Canted Trestles, Louis Mozerolles' Joiners Table, Sawhorses, and the Saint Andrews' Cross, twisted crosses. You'll also find theories on hip rafter shift-offset, standard roof framing kernel trait drawings, German Schiften DP-Shadow Line techniques, folding net roof surface and net plane geometric development, when hip rafters collide, the Warlock Cut, and developing upper and lower claws on rafters using Axioms.
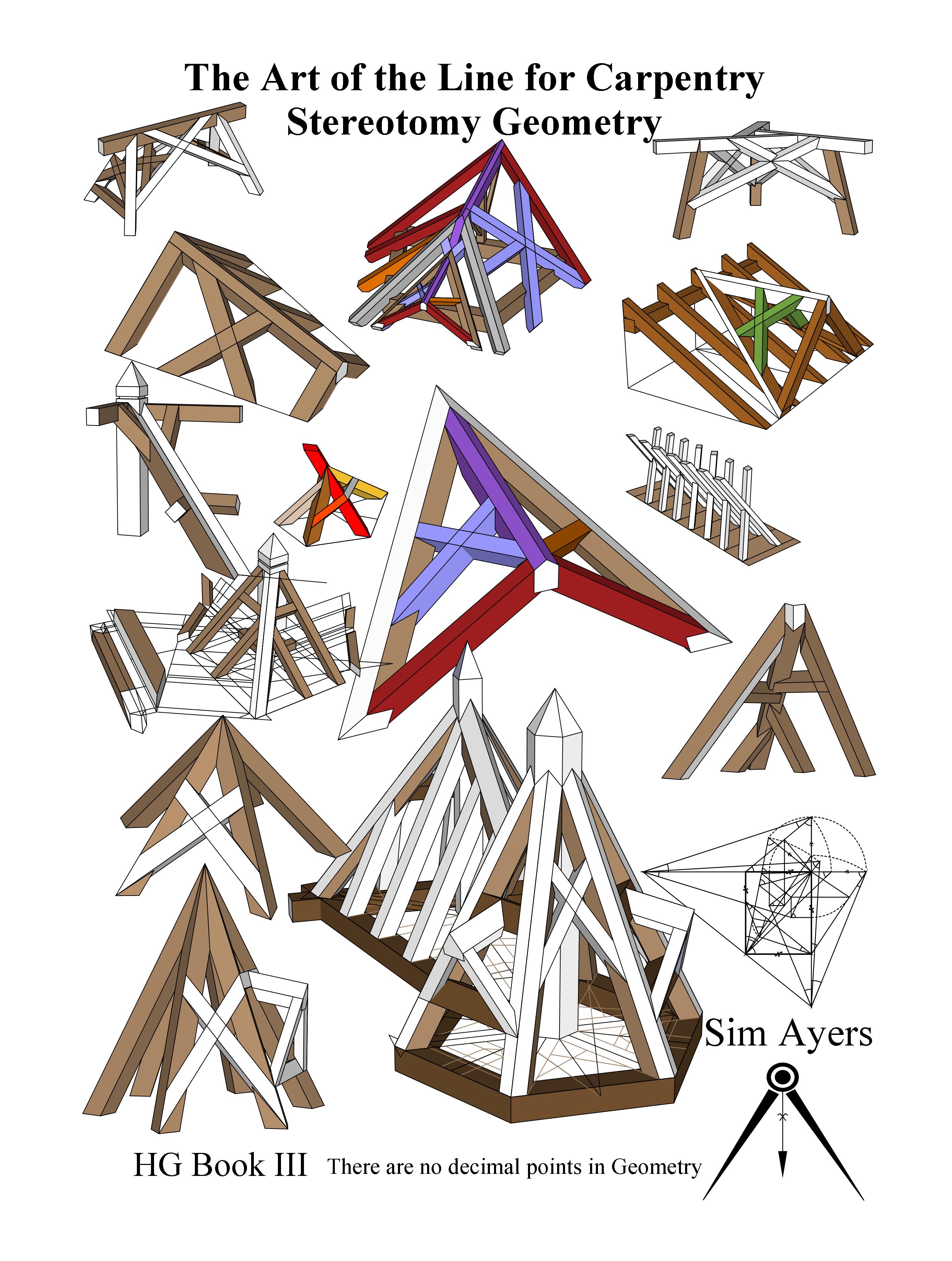
The book includes step-by-step instructions on developing stereotomic double curvature drawings for circular work in carpentry. Some of the techniques presented in this book are thousands of years in the making. As carpenters, we shouldn't have to re-invent the wheel each time we are faced with new challenges. There is a likely hood that someone, that came before us, has already refined a technique that we can use today. The tools might have changed, but the piece of wood that it is twisting and turning remains the same piece of wood.

Rafter Tools+ is a rafter calculator for complex roof framing angles that other roof framing calculators don't offer.

This iPhone app is for rough frame carpenters that don't build stairs everyday, but could use an stair app calculator to check their stair building calculations.
Build a set of stairs that you are gonna be proud of.
With Stair Tangent you can elimenate cumulative math errors when building - constructing stairs.

Crown Molding Tools
crownmoldingtools.com