
Treatise On Those Parts of Geometry Needed by Craftsmen |
|
| Sand Geometry Light Geometry Egyptian Geometry Greek Geometry Roman Geometry Arabic/Islamic Geometry Persian Geometry Pythagoras Geometry Euclidean Geometry Vitruvian Geometry Archimedes Geometry Apollonios Geometry Sacred Geometry Vesica Piscis Geometry Ad Triangulum Geometry √3 Geometry Ad Quadratum Geometry √2 Geometry Golden Ratio phi = (√5 + 1) ÷ 2 ) = 1.6180339887 |
Ad Triangulum ( triangle within the circle) Ad Quadratum (square within the circle) |
| The circle, and its centre, are the point at which all Geometry
begins. From the circle comes three fundamental figures in Geometry, the triangle, square and hexagon. |
|
| The ellipse, and its centre, are the point at which all Elliptical
Geometry begins. By plotting abscissas and ordinates of the sun's shadow, you can drive the chariot of the sun's arc south of the equator to see the chariot of light at winter solstice. |
|
Philibert De l'Orme, LE TROISIEME LIVRE DE L’ARCHITECTURE
Six kinds of lines or geometric figures extracted from Euclid and Archimedes. The first kind will be used for all runs and vaulted cellars strange as they please, as we have said and shown at the beginning of the third book, the other will be used to find all kinds of arches and doors, and the third for all tubes, and the fourth for all kinds of spherical vaults and other developments, the fifth for all ways of stairs, and the sixth for all kinds of screws. |
|
This work contains the science and practice of construction geometry in a simple and familiar manner for the advantages of readers not yet acquainted with geometry or trigonometry, no more trigonometry has been employed than was absolutely necessary. And further, there is always danger of overstocking the average craftmen’s storehouse of knowledge, the result of which tends to confuse and produce errors.
Polygon Rafter Tables
3 Sided Polygon Rafter Table
4 Sided Polygon Rafter Table
5 Sided Polygon Rafter Table
6 Sided Polygon Rafter Table
7 Sided Polygon Rafter Table
8 Sided Polygon Rafter Table
9 Sided Polygon Rafter Table
10 Sided Polygon Rafter Table
11 Sided Polygon Rafter Table
12 Sided Polygon Rafter Table
16 Sided Polygon Rafter Table
24 Sided Polygon Rafter Table
32 Sided Polygon Rafter Table
36 Sided Polygon Rafter Table
42 Sided Polygon Rafter Table
48 Sided Polygon Rafter Table
64 Sided Polygon Rafter Table
96 Sided Polygon Rafter Table
Use of the Framing Square for Octagonal Roofs
Octagon Framing Square usage: 3:12 Pitch
Octagon Framing Square usage: 4:12 Pitch
Octagon Framing Square usage: 5:12 Pitch
Octagon Framing Square usage: 6:12 Pitch
Octagon Framing Square usage: 7:12 Pitch
Octagon Framing Square usage: 8:12 Pitch
Octagon Framing Square usage: 9:12 Pitch
Octagon Framing Square usage: 10:12 Pitch
Octagon Framing Square usage: 11:12 Pitch
Octagon Framing Square usage: 12:12 Pitch
Polygon Rafter Tables all in one PDF file
Polygon Rafter Tables
Eagle Square Manufacturing Co., (South Shaftsbury, Vt.),the Octagon Framing Square that real
roofers used !
Eagle Framing Square -- invented in 1814
HAWES PAT
Silas Hawes made squares in Shaftsbury, VT, 1814 - 1828, but that several other local makers
also marked their squares "HAWES PAT". These were predecessors to the famous Eagle Square Co. organized in 1859. A
fine example of a used hand forged, hand stamped square of the early days of the republic.
Picture of Eagle Octagon Framing Square
Picture of similar Octagon Framing Square
PDF files of geometry construction for Treatise On Those Parts of Geometry Needed by Craftsmen.
|
Treatise On Those Parts of Geometry Needed by Craftsmen
Treatise On Those Parts of Geometry Needed by Craftsmen 
|
|
Double Curvature Arch Geometric Development
Intersection of Vertical and Horizontal Cylinders Double Curvature Arch  
|
|
Square Groin Vault
With Transverse and Longitudinal ribs Semi-circular Quadripartite vaulting with equal height ordinates Square Groin Vault 
|
|
Square Groin Vault Segmental Arches
With Transverse and Longitudinal ribs with segmental arches Quadripartite vaulting with equal height ordinates Square Groin Vault Segmental Arches 
|
|
Rectangular Segmental Arch Groin Vault
With Transverse and Longitudinal ribs with segmental arches Quadripartite vaulting with equal height ordinates Rectangular Segmental Arch Vault 
|
|
Square Gothic Vault with Elliptic Cross Diagonals
With Transverse and Longitudinal ribs being Gothic Arches Quadripartite vaulting with equal height ordinates Square Gothic Vault with Elliptic Cross Diagonals 
|
|
Rectangular Gothic Vault
With Transverse and Longitudinal ribs with Gothic Arches Quadripartite vaulting with equal height ordinates Rectangular Gothic Arch Vault 
|
|
Octagon vaulting with Equal Side Lengths
With Transverse ribs Semicircular Octopartite vaulting with equal height ordinates Octagon vaulting with Equal Side Lengths Semicircular 
|
|
Octagon vaulting with Equal Side Lengths
With Transverse ribs Segmental Octopartite vaulting with equal height ordinates Octagon vaulting with Equal Side Lengths Segmental 
|
|
Octagon vaulting with Equal Side Lengths
With Transverse ribs Gothic Octopartite vaulting with equal height ordinates Octagon vaulting with Equal Side Lengths Gothic 
|
|
Hexagon vaulting with Equal Side Lengths
With Transverse ribs Lancet Gothic with equal height ordinates Hexagon vaulting with Equal Side Lengths Lancet Gothic 
|
|
Dodecagon vaulting with Equal Side Lengths
With Transverse ribs Lancet Gothic with equal height ordinates Dodecagon vaulting with Equal Side Lengths Lancet Gothic 
|
|
Domical - Spherical Vault on Square base
With Cross Diagonal ribs Semicircular With Transverse ribs Semicircular ( Sail Vault ) Hemispherical Dome Vault Domical - Spherical Vault on Square base Semicircular 
|
|
True Gothic Vault with arc's forming all of the ribs from the book
ROBERT WILLIS ON THE CONSTRUCTION OF THE VAULTS OF THE MIDDLE AGES (1842) Fig. 10 page 13 With Transverse vault ribs, Longitudinal vault ribs stilted, Cross Diagonal ribs, Tierceron ribs are all arc's. Willis shows how none of the ribs are drawn from ordinates like the Roman and Italian groined vault. Willis proclaims that Philibert de I'Orme, Maturin Jousse, Derand, De la Rue, Frezier, William Halfpenny and Peter Nicholson were all miss guided by masonic projection techniques. True gothic vaults used only arc's not ellipses from ordinate projection. ROBERT WILLIS ON THE CONSTRUCTION OF THE VAULTS OF THE MIDDLE AGES 
|
|
Elliptical Surface Development of Barrel Vault Surface
with equal height ordinates Elliptical Surface Development of Barrel Vault Surface 
|
|
Surface Development of Cone
Surface Development of Cone 
|
|
Tangent To Circle
Tangent To Circle 
|
|
Dihedral Angle of Tetrahedron
Equilateral Triangular Pyramid Dihedral Angle = 70.52878°
Tetrahedron Angles
90-D Angle = 60.00000
Hip Backing Angle = arctan( sin( Hip Pitch Angle) ÷ tan( Plan
Angle ) ) Dihedral Angle = ( 90° - Hip Backing Angle ) * 2 The dihedral angle is the angle measured between two planes. |
|
Dihedral Angle of Rectangular Pyramid Roof
Major Pitch Angle = 39.81° Minor Pitch Angle = 33.69° Hip Pitch Angle = arctan( tan( Pitch Angle ) * sin( Plan Angle )) Hip Backing Angle = arctan( sin( Hip Pitch Angle) ÷ tan( Plan
Angle ) ) Dihedral Angle = 180° - 29.99° -20.27° = 129.74°
|
Rectangular Pyramid Roof With Square Tail Fascia Geometric & Trigonometric
Roof Framing Development
Deck Angle = 90.00000 Rectangular Pyramid Roof With Square Tail Fascia Geometric & Trigonometric Roof Framing Development |
Treatise on Stair Building & Handrailing Twist Bevel Angle Geometric Development based on Tetrahedron of Triangular Pyramid |
| Helix Geometric Development
Circumference = pi x Diameter Length of Helix = sqrt (pi x Number of Turns x Diameter)^2 + (Length^2) Helix Geometric Development 
|
| Dome on Octagonal Pyramidal Roof using equal height ordinates for geometric development.
Dome on Octagonal Pyramidal Roof Geometry 
|
| Ellipse Geometric Development with Radical Lines
.
Ellipse Geometric Development with Radical Lines 
|
| Cone Surface Geometric Development.
Cone Surface Geometric Development 
|
Barrel Vault Intersects Main Roof Vertical & Horizontal Trace Development. If a line be perpendicular to an oblique plane, the projections of the
line are |
| Equal Sided Octagon Geometric & Trigonometric Roof Framing Development Pitch Angle = 33.69° Plan Angle = 67.5° Hip Rafter Pitch Angle = arctan( tan( Pitch Angle ) * sin( Plan Angle
)) = 31.63° Jack Rafter Side Cut = arctan( cos( Pitch Angle ) ÷ tan( Plan
Angle )) = 19.01° Roof Sheathing Cut Measurement = Plywood Width ÷ tan( Roof Sheathing
Angle) = 16.54" Frieze Block Saw Miter Angle = arctan( sin ( Pitch Angle ) ÷ tan(
Plan Angle )) = 12.94° Common Rafter Rise = Run * tan( Pitch Angle ) Hip Rafter Run = Run ÷ cos( Plan Angle ) Equal Sided Octagon Geometric & Trigonometric Roof Framing Development 
|
Polygon 2 Cord Gables ( Prow Rafters ) can be calculated with the same angles used to calculate the polygon rafters. The working angle of the polygon is used to calculate the length of the 2 Cord Gable. The length of the 2 Cord Gable is calculated using the following formulas. Example: side wall length = 59.64696 common rafter length = common rafter run ÷ cos ( pitch angle ) hip rafter length = hip rafter run ÷ cos ( hip pitch angle ) polygon gable rafter length = hip rafter length Mark the gable rafter at the same pitch angle as the hip pitch angle on the gable rafter material. Then cut the head cut angle with your saw set at the polygon miter angle. The Octagon polygon miter angle is 22.5°. The saw bevel angle is the same as the polygon miter angle. The polygon 2 cord gable rafter (prow rafter) is calculated at the same pitch angle as a polygon hip rafter.
Polygon 2 cord gable rafter (prow rafter)
Geometric & Trigonometric Roof Framing Development |
| Tetrahedron Developmental Geometric & Trigonometric Developmental drawings for Crown Molding with 38° Spring Angle .
Crown Molding with 38° Spring Angle Geometry 
|
| Tetrahedron Developmental Geometric & Trigonometric Developmental drawings for 8:12 pitched roof.
Tetrahedron Developmental Geometric & Trigonometric Developmental drawings for 8:12 pitched roof 
|
| Canadian & American Geometric Roof Framing Development & Framing Square Usage.
Canadian & American Geometric Roof Framing Development & Framing Square Usage Tetrahedron Calculator Canadian & American Geometric Roof Framing Development & Framing Square Usage 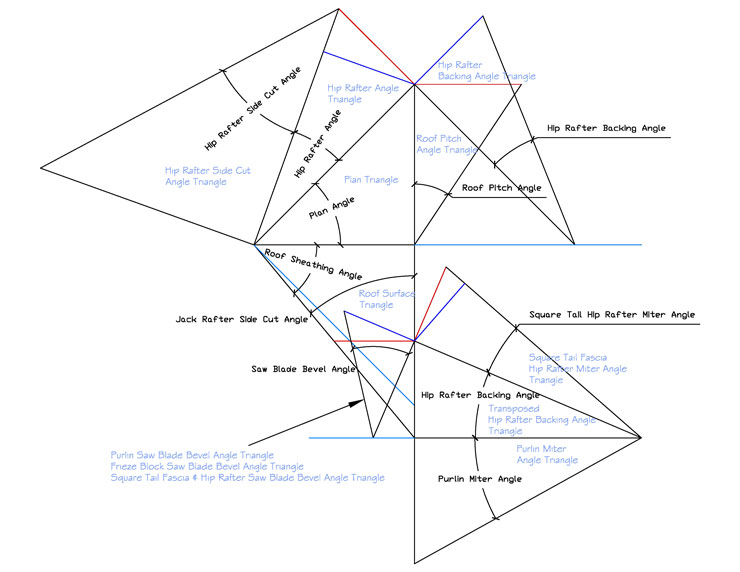
|
| Irregular hip roof Geometric & Trigonometric Developmental drawings for 6:12 - 12:12 pitched roof & Framing Square Usage.
Irregular hip roof Geometric & Trigonometric Developmental drawings for 6:12 - 12:12 pitched roof 
|
| Roof Framing Kernel drawing for visualization posterboard cut out model .
Roof Framing Kernel drawing for visualization posterboard cut out model 
|
Ellipse Formulas for Eyebrow Roof Design Intersecting Slope Angle = arctan((Roof Pitch - Dormer Pitch ) ÷
12) |
| Ad Triangulum based on three point geometry, Medieval Cathedral Framing based on Ad Trianguluml Geometry.
Ad Triangulum 3 point Geometry 
|
| Ad Triangulum based on six point geometry, Medieval Cathedral Framing based on Ad Trianguluml Geometry.
Ad Triangulum 6 point Geometry 
|
| Vitruvius - Ptolemy Alalemma Sundail from 12 point geometry and orthographic projection of ellipse.
Elliptical Sundial Geometry 
|
| Vitruvius The Alalemma Sundail and Its Applications Book 8,Chapter 7
Vitruvius Alalemma Sundail Geometry for Latitude 37.91° 
|
| Construction Of Gothic Window with Oculus Based on Euclid's Elements Book 1 Prop 1
Gothic Window with Oculus 
|
| Equilateral Gothic Arch Construction Based Euclid's Elements Book 1 Prop 1
Equilateral Gothic Arch 
|
| Six Point Geometry, Euclidean Geometry, Seed Of Life, Hex Rose Pedal,Daisy Wheel, Thunder Marks, Construction Based Euclid's Elements Book 1 Prop 1
Six Point Geometry, Euclidean Geometry, Seed Of Life, Hex Rose Pedal,Daisy Wheel, Thunder Marks 
|
| Square Construction Based Euclid's Elements Book 1 Prop 1
Square Construction 
|
| Pentagon Construction Based Euclid's Elements Book 1 Prop 1
Pentagon Construction 
|
| Equilateral Arch Construction Based Euclid's Elements Book 1 Prop 1
Equilateral Arch 
|
| Elliptic Gothic Cross Vault Arch Construction Based Euclid's Elements Book 1 Prop 1
Elliptic Gothic Cross Vault Arch 
|
| Euclid's Elements Book 1 Prop 47 In right-angled triangles the square on the side opposite the right angle equals the sum of the squares on the sides containing the right angle.
Euclid's Elements Book 1 Prop 47 
|
| Philibert De l'Orme, LES LIVRES D'ARCHITECTURE
Squaring the Foundation with Equilateral Triangles Take the case that you have drawn the line QR, and hereunto an equilateral triangle, that is to say as great on one side than the other, as you see RST, T is the point where you pull another curved line marked Z, is tightened without moving the compass, and requires that the distance ST is similar to that of TZ. This makes you draw a straight line from point S to T, till it intersects the line Z, and this place, as you see the point marked X, you draw another line even to the point of R, which will be precisely perpendicular to the line QR, as you can judge by the figure followed. Philibert De l'Orme, LES LIVRES D'ARCHITECTURE, Squaring the Foundation with Equilateral Triangles Geometry 
|
| The flat plane surfaces of the Platonic Solids are the triangle, square, and pentagon.
Platonic Equilateral Triangle, Square, Pentagon Geometry 
|
| Pyriamd Geometry with phi Golden Ratio phi = (√5 + 1) ÷ 2 ) = 1.6180339887
Pyriamd Geometry with phi 
|
| Vitruvius Greek Theater based on Square,Ad Quadratum Geometry,Book 5,Chapter 7
Vitruvius Greek Theater based Ad Quadratum Geometry 
|
| Philibert De l'Orme, LES LIVRES D'ARCHITECTURE
Wind Direction of the four corners of the world. Rotated Squares Ad Quadratum Geometry Chapter 7
Of these four main parts of the world four winds blowing directly appointed principal
or cardinal knowledge is the point of East Subsolanus, marked the ensuing Figure A,
where the quality and nature is hot and dry in the West Favonius sale, noted by C,
its quality being cold and moist, Midi, Auster, signed B,
whose nature and quality wet and hot and Septentrion Boreas, marked D,
where quality is cold and dry.
Philibert De l'Orme, LES LIVRES D'ARCHITECTURE, Ad Quadratum 8 point Geometry Philibert De l'Orme, LES LIVRES D'ARCHITECTURE, Ad Quadratum 16 point Geometry 
|
| Vitruvius Roman Theater based Triangle, Ad Triangulum Geometry, Book
5,Chapter 6 Chapter 5 1. The foundation should be of the soundest workmanship and materials, and of greater thickness than the walls above. 2.The plan of a city should not be square, nor formed with acute angles, but polygonal. 3. The thickness of the walls should be sufficient for two armed men to pass each other with ease. 4. The distance between each tower should not exceed an arrow's flight. 5. The towers should be made either round or polygonal.
Vitruvius Roman Theater based Triangle, Ad Triangulum Geometry
|
| Daisy Wheel based on six point geometry, Timber Framing based on Daisy Wheel Geometry
Timber Framing based on Daisy Wheel Geometry 
|
| Golden Ratio phi Geometry, Two Story Framing based on Golden Ratio, Golden Ratio Geometry
based on equilateral triangle inscribed in circle,Golden Ratio Geometry based on pentagon inscribed in circle
Golden Roof Slope Angle 31.72° 
|
| Gothic Arch Semi-Major Radius for a 67.5° Plan Angle, 60° Plan Angle, 45° Plan Angle, 30° Plan Angle Geometry
Gothic Arch Elliptical Cross Vault Hip Drawn with Height Ordinates Geometry 
|
| Gothic Arch Types Geometry,Standard Gothic Arch with Radius equal to width of opening, Lancet Gothic Arch with Radius bisecting radius cord and spring line of opening
Lancet Gothic Arch Types 
|
| Octagon Rosette Geometry
Octagon Rosette 
|
| Descriptive Geometry for Drawing an Octagon, Sacred Cut
Octagon Geometry 
|
| Descriptive Geometry for Drawing an Octagon from side length of Octagon
Octagon from side length of Octagon Geometry 
|
| Descriptive Geometry for Octagram
Octagram Geometry 
|
| Bisect Angle using a Compass and Straight Edge
Bisect Angle using a Compass and Straight Edge 
|
| Descriptive Geometry, How To Draw Oval for Elliptical Cross Vaults Using only Compass and Straight Edge
How To Draw Oval for Elliptical Cross Vaults Using only Compass and Straight Edge 
|
| Gothic Cross Vault, Elliptical Cross vault diagonals drawn with co-centric circles and orinadtes.
co-centric circles and orinadtes 
|
| Gothic Arch from vesica piscis
Gothic Arch from vesica piscis 
|
| Gambrel Roof Design Geometry from Dutch Hexagram - Rotated Hexagons
Gambrel Roof Design 
|
| Philibert De l'Orme, LES LIVRES D'ARCHITECTURE
Speed Square or Angle Dial with an Equilateral Triangle Ad Triangulum Geometry Be given an equilateral triangle such width as you like, like ABC, the more it grows, so will the insurance and kindness. Where do I did not wish to help more than that which you see below figuratively, by as much as I used to be easier in my coffers, and do not usually point thereof, a Astrolable be, and ephemeris, with a few other books, and cases filled compass, and what it takes to portraire. Within this triangle imagine a circle, as you can see marked EFGH (almost as if it were a dial showing the hours) and divide into so many parts that will, like twenty-four, thirty-two, forty eight, the most that there is the best. I divided the latter into thirty-two, and is set amidst a magnetic needle, as well as marine dials and compasses, or small whom we help to find the hours to the Sun, but notice that said needle must be very good and very moving. When you want to help the triangle, you look through one side as you please, for the one marked in Figure D. This makes you discard your city view, castle or place from which you want to take the form and figure, and make a sketch first on paper scored coarsely and you can understand the decision. Can you make the trip at all. If you want that it should fit in memory or writing a bend and each face of the walls to measure the length as you will see below. Having done this, you can start at one end of the castle, town or place, keeping your triangle against the first section of wall with a ruler to have greater decision, against which must be your triangle as you see marked K. Philibert De l'Orme, LES LIVRES D'ARCHITECTURE, Angle Dial with an Equilateral Triangle Geometry 
|
| Philibert De l'Orme, LES LIVRES D'ARCHITECTURE
Plumb Bob from an Equilateral Triangle Ad Triangulum Geometry Philibert
De l'Orme, LES LIVRES D'ARCHITECTURE, Plumb Bob from Equilateral Triangle
Geometry |
| Philibert De l'Orme, LE TROISIEME LIVRE DE L’ARCHITECTURE
The three lost points of the circle geometry and lengthened arch I suggest you put three points to your will, and that from one point to another you draw the lines, you divide that by the middle, and then made a perpendicular thereon, and you see the two lines A and B and where they meet and intersect is the center and you see the place where is C, where you have to put one of the points of the compass, and mark another line precisely, which will go on three points, as you can see in figure marked C in the center. You can also proceed in this case with the compass by the way you see kept in the following figure given, which is way more secure. So that those who are quick to wield said compass, do not square, as well as if it is just and right, the line can not be done precisely. So looking to find the lengthened with the three points is very useful and necessary, because you can not only do not lift a panel to a building on a round shape, it must always find you are looking lengthened, which can not be done quickly if not by those three points lost, they are in the panel as those marked D and I said, and are looking more and different. Philibert De l'Orme, LES LIVRES D'ARCHITECTURE, The three lost points of the circle geometry and lengthened arch 
|
| Philibert De l'Orme, LE TROISIEME LIVRE DE L’ARCHITECTURE
Geometric features that show as it is cut and cut the stones to make the doors and down the basement and floors that are in the land, such as kitchens, baths, bathe, and similar where you can go to level, and it must descend. Philibert De l'Orme, LES LIVRES D'ARCHITECTURE, Sloped basement cellar Vault geometry 
|
| Philibert De l'Orme, LE TROISIEME LIVRE DE L’ARCHITECTURE
Modern vaults, the master masons were accustomed to churches and homes of the nobles. Philibert De l'Orme, LES LIVRES D'ARCHITECTURE, Modern Cross Vault geometry 
|